Метод интерпретации результатов измерений параметров речевого сигнала в задачах диагностики психоэмоционального состояния человека по его речи
Аннотация
Предложены структура устройства диагностики и метод интерпретации данных измерений параметров речи, основанный на информационном подходе. Описан алгоритм обучения интерпретирующего устройства на основе принципа максимума информации и приведены результаты экспериментов по обучению. Обсуждены перспективы дальнейших исследований.
Ключевые слова: диагностика, речь, информационный подход, принцип максимума информации.05.11.17 - Приборы, системы и изделия медицинского назначения
05.12.04 - Радиотехника, в том числе системы и устройства радионавигации, радиолокации и телевидения
Диагностика состояния человека находит сегодня все более широкое практическое применение в различных областях медицины, техники, науки и других. Важным частным случаем данного класса задач является диагностика психоэмоционального состояния человека по его речи. В ряде случаев, когда доступен лишь речевой канал связи (диагностика пилотов, диспетчеров), эта задача приобретает первостепенное значение, в других случаях, например, при диагностике психоэмоционального состояния больных в стационаре, аппаратный анализ речи может использоваться как вспомогательный метод диагностики.
Аппаратной диагностике психоэмоционального состояния человека по его речи было посвящено немало работ, краткий обзор некоторых из них приведен в [1]. Можно выделить три ключевых вопроса, которые так или иначе возникают в исследованиях такого рода:
1) какие параметры речевого сигнала следует измерять;
2) каким образом измерить выбранные параметры;
3) как интерпретировать результаты измерений в терминах психоэмоционального состояния человека.
Как правило, в исследованиях основное внимание уделяется первым двум вопросам. Измеряются спектральные [2], временные [3], кепстральные и иные [4] параметры речевого сигнала. В плане техники и методологии измерений параметров достигнуты значительные успехи: так при измерении параметров, воспринимаемых слухом человека (громкость, спектральные и временные характеристики), точность аппаратных измерений может многократно превосходить возможности слуха. В то же время точность диагностики психоэмоционального состояния с помощью аппаратных средств в общем случае не превосходит способности человека к оценке состояния другого человека по его речи. Возможно, это противоречие объясняется несовершенством подходов к решению третьей из указанных выше задач - интерпретации результатов измерений.
Как правило, в исследованиях связь между измеряемыми параметрами речи и параметрами состояния человека априорно считается линейной или приближенно линейной. Такое предположение вызывает определенные сомнения, хотя бы потому, что человеческий организм представляет собой сложную систему, компоненты которой связаны нелинейным образом.
Математический аппарат теории информации предлагает ряд характеристик, отражающих связь (не обязательно линейную) между двумя случайными величинами. К таким характеристикам могут быть отнесены: условная вероятность, совместная вероятность, взаимная информация.
Для интерпретации результатов измерений речевого сигнала в терминах психоэмоционального состояния человека возможно использование совместных вероятностей, отражающих связи между параметрами речи и параметрами состояния человека. Система интерпретации, работающая по такому принципу, не будет ограничена априорным представлением о линейном характере этих взаимосвязей. Для получения совместных вероятностей потребуется предварительное обучение системы.
Структурная схема устройства для диагностики психоэмоционального состояния человека по его речи показана на рис. 1.
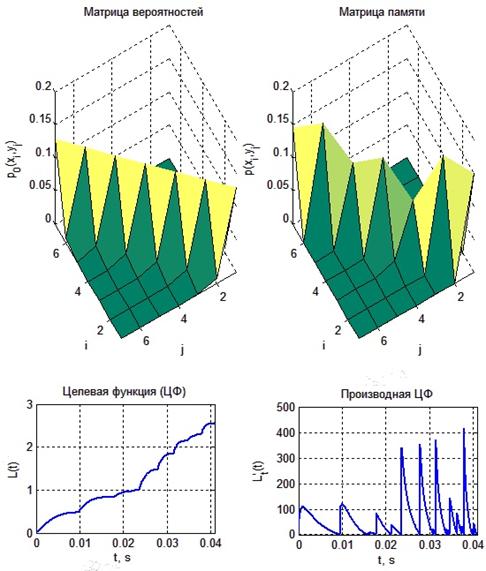
Речевой сигнал от источника поступает в измерительный блок. Результаты измерения параметров речи представляются в виде дискретных распределений вероятностей p(Xn) значений этих параметров.
 |
|
Рис.1 Структурная схема системы диагностики психофизиологического состояния человека по его речи |
На рис. 2 представлено распределение на нормированном интервале значений параметра от –1 (минимальное значение параметра) до 1 (максимальное значение параметра).
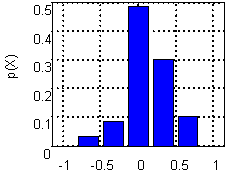
Рис. 2 Вектор вероятностей значений параметра речи X
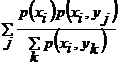 .
.
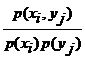 .
.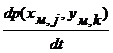 =aj,k(p(xм,j)p(yм,k) – p(xм,j, yм,k)),
=aj,k(p(xм,j)p(yм,k) – p(xм,j, yм,k)),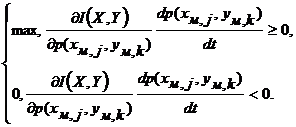
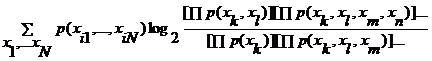 ,
,